作者: 徐子杰 王燕
单位: 南京工业大学机械与动力工程学院
引用: 徐子杰 , 王燕 . 多孔基无机复合相变材料的蓄热特性 [J]. 储能科学与技术 ,2022,11(10):3171-3179.
DOI : 10.19799/j.cnki.2095-
4239.2022.0070
1 物理模型
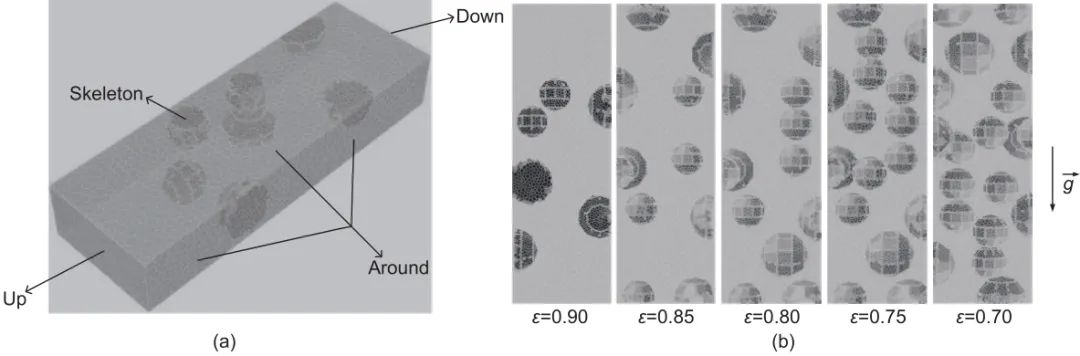
表1 六水氯化钙热物性参数

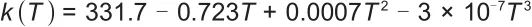
|
(1) |
2 数值计算方法
2.1 模型假设与控制方程
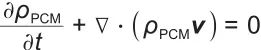
|
(2) |
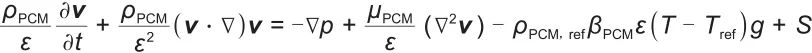
|
(3) |
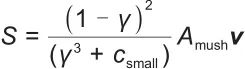
|
(4) |
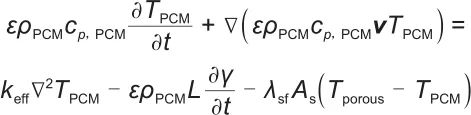
|
(5) |
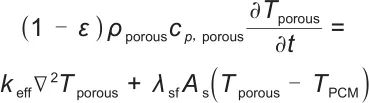
|
(6) |
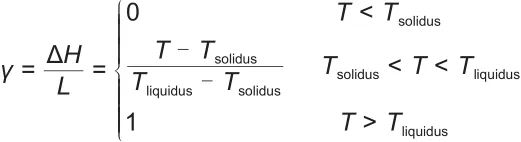
|
(7) |
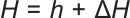
|
(8) |
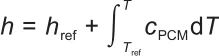
|
(9) |
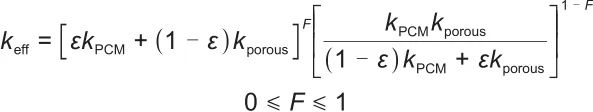
|
(10) |
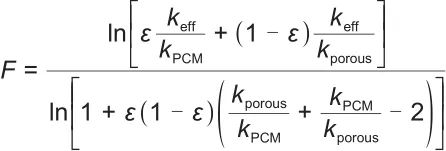
|
(11) |
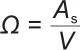
|
(12) |
2.2 边界条件及计算方法
2.3 模型验证
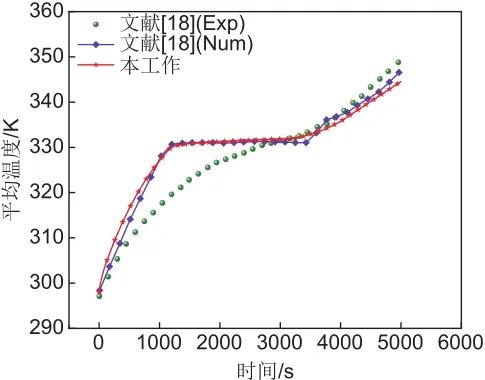
2.4 网格独立性分析
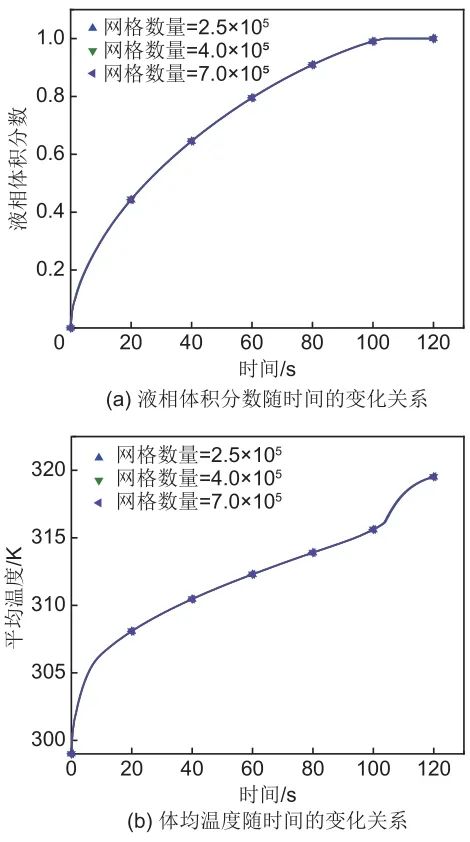
3 数值模拟结果与分析
3.1 孔隙度的影响
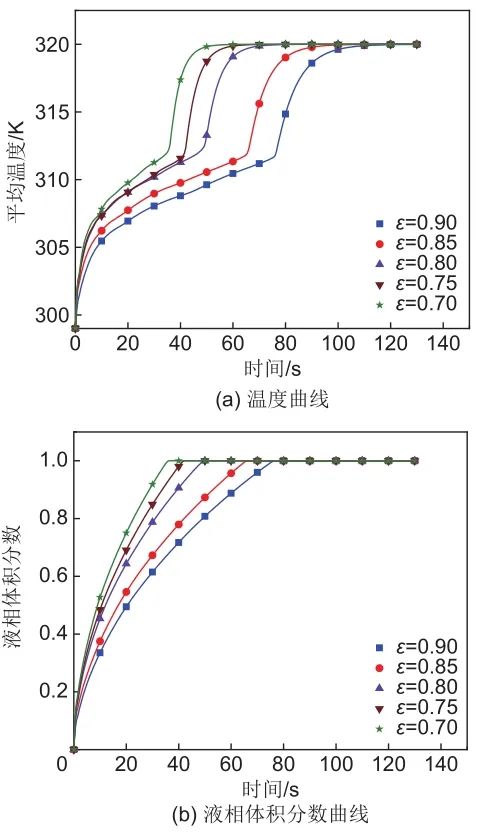
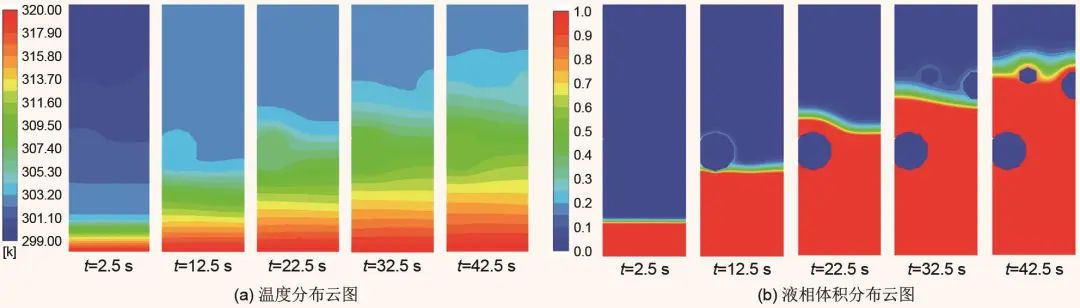
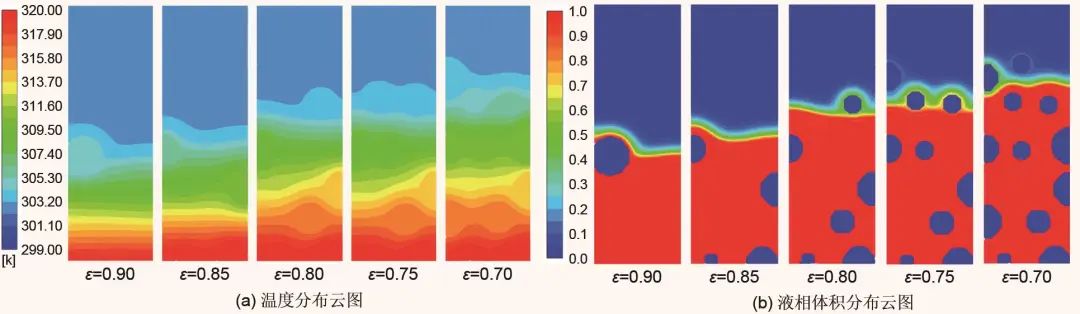
3.2 孔径的影响
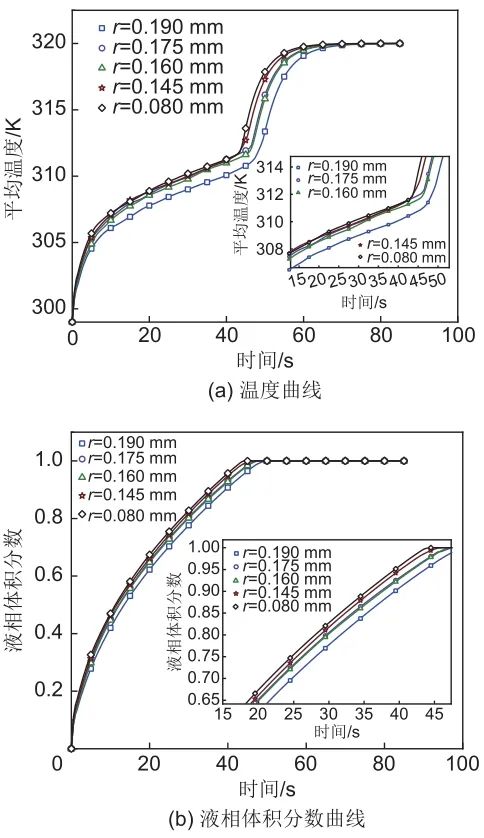
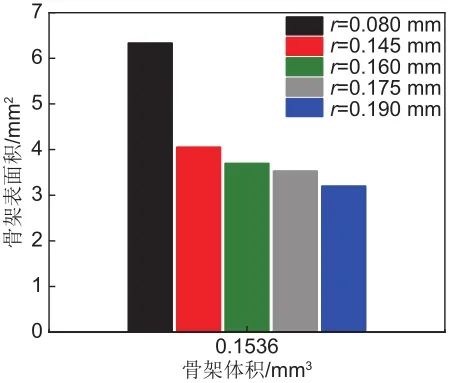
3.3 孔形貌结构的影响
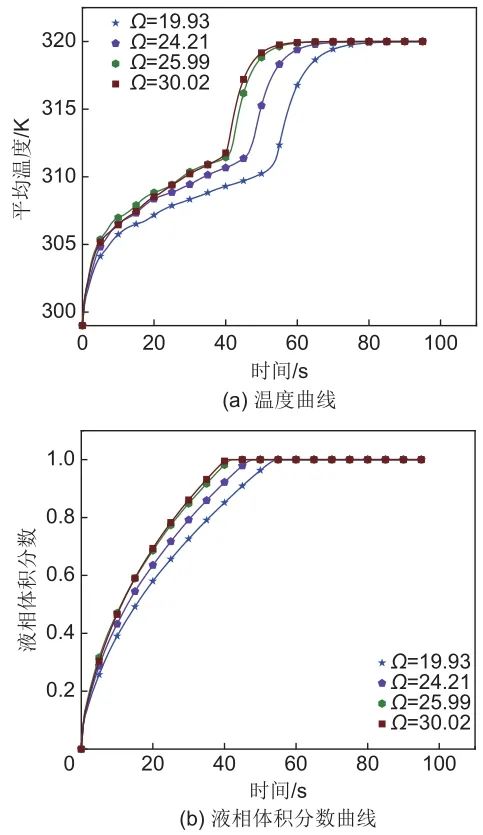
3.4 有效热导率与蓄热能力
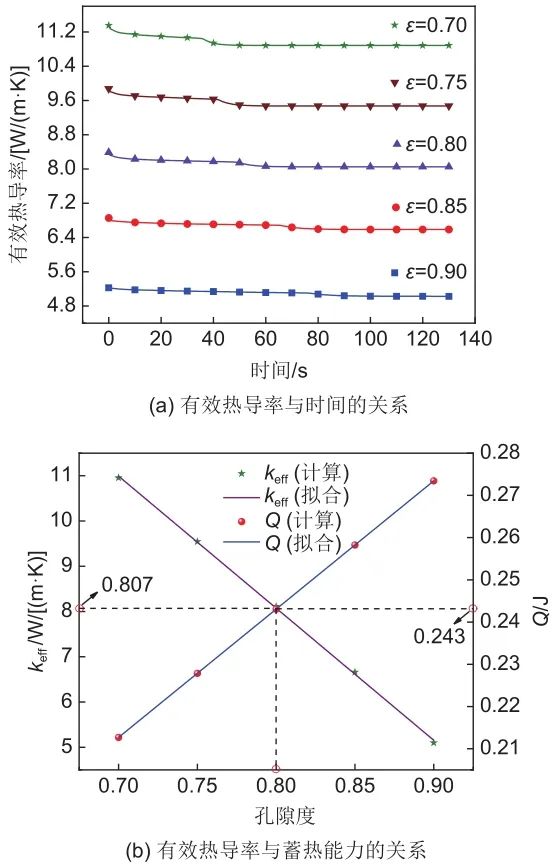
4 结论
符号说明
| 符号 | —— | 符号说明 |
|---|---|---|
| A | —— | 表面积,mm 2 |
| c p | —— | 比热容,kJ/(kg·K) |
| g | —— | 重力,m/s 2 |
| h | —— | 比焓,kJ/kg |
| k | —— | 热导率,W/(m·K) |
| L | —— | 相变潜热,kJ/kg |
| p | —— | 压强,Pa |
| Q | —— | 蓄热量,J |
| S | —— | 源项 |
| T | —— | 温度,K |
| t | —— | 时间,s |
| v | —— | 速度矢量 |
| V | —— | 体积,mm 3 |
| β | —— | 膨胀系数 |
| γ | —— | 液相体积分数 |
| ρ | —— | 密度,kg/m 3 |
| ε | —— | 孔隙度 |
| λ | —— | 换热系数,W/(m 2 ·K) |
| μ | —— | 动力黏度,Pa·s |
| Ω | —— | 比面积,mm -1 |
| 下角标 | ||
| eff | —— | 有效值 |
| PCM | —— | 相变材料 |
| porous | —— | 多孔介质 |
| solidus | —— | 固相 |
| liquidus | —— | 液相 |
第一作者: 徐子杰(1996—),男,硕士研究生,研究方向为储热技术,E-mail:XZJ_;
通讯作者: 王燕,副教授,研究方向为高效换热和储能技术,E-mail:。
专刊推荐
(点击图片即可跳转到相应文章合集)






